公務員考試培訓網

　　關于牛吃草問題，很多同學都是用公式法，但是大部分同學在即公式的過程中，容易記混，另外，在稍微復雜的問題面前，套公式也容易搞錯，在此，就該問題做一下解析，希望能給大家提供一點幫助。

　　例1 一牧場上的青草每天都勻速生長。這片青草可供27頭牛吃6周，或供23頭牛吃9周。那么可供21頭牛吃幾周？

　　這是一道典型的牛吃草問題。關于牛吃草問題，有一個很經典的公式，就是：

　　草場原有草量=(牛數-每天長草量)×天數

　　一、關于對公式的理解

　　關于以上這個公式，很多同學不太理解。其實這個公式可以從追及問題的角度出發理解：

　　追及距離=(大速度-小速度)×追及時間

　　在這個問題中，

　　1、原有草量相當于追及距離，

　　2、(牛每天吃草量-每天長草量)相當于(大速度-小速度)，假設每頭牛每天吃草量為1，則可寫成(牛數-每天長草量)

　　3、天數就是追及時間

　　所以，草場原有草量=(牛數-每天長草量)×天數

　　二、另外一個思路

　　另外，有些同學總覺得公式不好記，或者時間一長就容易記混，也可以從理解的角度出發簡單地列出方程組來：

　　首先：草的消耗量=草的供應量，而草的消耗量就是牛吃草的總量，即

　　牛吃草的總量=草場供應草的總量，即

　　牛數×天數×每頭牛每天吃草數=草場原有草量+新長草總量，即

　　牛數×天數×每頭牛每天吃草數=草場原有草量+天數×每天新長草量

　　其中，紅色部分均為未知數，又因為他們都屬于草量單位，所以，他們之間的關系是比例關系，不是絕對數關系，這樣，我們就可以把每頭牛每天吃草量設為1，每天新長草量設為x，草場原有草量設為y；則有：

　　牛數×天數×1=y+天數×x

　　三、解題

　　則，根據以上公式，設所求天數為n，例1可以列出以下方程組：

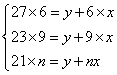
　　從1、2個方程中解出x=15，y=72，代入第3個方程，可解出n=12

　　同樣，下例也可以如法炮制：

　　例2 某車站在檢票前若干分鐘就開始排隊，每分鐘來的旅客人數一樣多。從開始檢票到等候檢票的隊伍消失，若同時開5個檢票口則需30分鐘，若同時開6個檢票口則需20分鐘。如果要使隊伍 10分鐘消失，那么需同時開幾個檢票口？

　　假設，開始檢票前人數為y，每分鐘新來人數為x,所求檢票口為n，則有

　　解出x=3，y=60，n=9

　　例3某海港貨口不斷有外洋輪船卸下貨來，又不斷用汽車將貨物運走，如果用9輛車，12小時可以清場，如果用8輛車，16小時也可以清場。該廠開始只用3輛車，10小時之后又增加了若干輛車，再過4小時就已清場，那么后來增加的車數應是？

　　假設每小時卸貨單位為x，原有存貨量為y，后增加的車輛數為n，則：

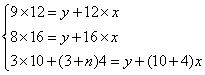
　　解出x=5，y=48，n=19