云南:2010年大學生村官行測備考指津二
來源:網絡 發布時間:2010-05-19 [an error occurred while processing this directive]
●數量關系常考規律之二:整除法
▲整除法
整除法利用的前提:
題目中的條件如果符合以下的要求:
= ,其中:A、B、m、n均為正整數,且m與n互為質數,則:A必為m的倍數,B必為n的倍數,A+B必為m+n的倍數,A-B必為m-n的倍數。根據這一結論,將能被整除的選項選出來,或者先將不能被整除的選項排除,然后再將其余的選項帶入排除。
真題一:
已知甲、乙兩人共有圖書260本,其中甲的書有13%是專業書,乙的書有12.5%是專業書,問甲有多少本非專業書( )。
A. 75 B. 87 C. 174 D. 67
【解析】B。根據條件“甲有專業書13%”,可知:
= ,故甲非專業書的數量一定是87的倍數,只能選擇B(87)或C(174)。(1)若甲的非專業書是87本,則甲的專業書是13本;則乙的專業書是(260-87-13)×12.5%=20本;(2)若甲的非專業書是174本,則甲的專業書是26本;則乙的專業書是(260-174-26)×12.5%=60×12.5%=7.5,非整數,舍棄。所以答案為B。
真題二:
某公司甲、乙兩個營業部共有50人,其中32人為男性,已知甲營業部的男女比例為5:3,乙營業部的男女比例為2:1,問甲營業部有多少名女職員?( )
A. 18 B. 16 C. 12 D. 9
【解析】C。由題目“32人為男性”知,女職員共有18人。根據:
=,=,故:甲男是5的倍數,甲女是3的倍數,乙男是2的倍數,乙女是1的倍數,總人數可以如下分配:甲男20人,甲女12人,乙男12人,乙女6人,與題目的條件吻合,故答案選C。
●數量關系常考規律之三:極值問題
極值問題的提問方式經常為:“最多”、“至少”、“最少”等,是行測試中出題頻率最高的題型之一。
一、本類試題基本解題思路如下:
1. 根據題目條件,設計解題方案;
2. 結合解題方案,確定最后數量;
二、常見設計解題方案原則如下:
(一)和固定
題目給出幾個數的和,求“極值”,解題方案為:如果求“最大值”,則:假設其余數均為最小,用和減去其余數,即為所求;如果求“最小值”,則:假設其余數均為最大,用和減去其余數,即為所求。
真題一:
100人參加7項活動,已知每人只參加一項活動,而且每項活動參加的人數都不一樣,那么,參加人數第四多的活動最多有幾個人參加?( )
A. 22 B. 21 C. 24 D. 23
【解析】A。這是一道“至多”問題。若要參加人數第四多的活動的人最多,則前三組的人數必須為1,2,3,并且后三組與第四多的人數必須依次相差最少。設第四多的人數為x,則后三組人數依次是x+1,x+2,x+3,則1+2+3+x+x+1+x+2+x+3=100,解得x=22。
真題二:
現有21朵鮮花分給5人,若每個人分得的鮮花數各不相同,則分得鮮花最多的人至少分得( )朵鮮花。
A.7 B.8 C.9 D.10
【解析】A。題目問“分得鮮花最多的人至少”可以分多少朵,則可以假設分得鮮花最少的到最多的依次為:x、x+1、x+2、x+3、x+m(其中:x+m是分得鮮花數最多的,但是只比前四個人多一點,即m﹥3),則列方程為:
x+x+1+x+2+x+3+x+m=21,得:5x=15-m
因為m﹥3,故m=5,所以x=2,
因此這5個人分得鮮花數可以為:2、3、4、5、7,故分得鮮花最多的人至少分7朵,也就是不能再少了。
第二部分 資料分析
●資料分析常考規律之一:增長率問題
增長率問題
增長率問題在資料分析中的表現形式主要有:***的增長率是多少?同比增長率是多少?環比增長率是多少?等等
涉及到的基本知識有:
百分數:提到增長率,就不能不提百分數,運用百分數時,要注意概念的精確。如“比過去增長20%”,即過去為100,現在是“120”;比過去降低20%,即過去是因為100,現在是“80”;“降低到原來的20%”,即原來是100,現在是“20”。
百分點:是指不同時期以百分數形式表示的相對指標,如:速度、指數、構成等的變動幅度。它是分析百分比增減變動的一種表現形式。例如,工業增加值今年的增長速度為15%,去年的增長速度為9%,今年比去年的增長幅度提高了7個百分點。今年物價上升了10%,去年物價上升了15%,今年比去年物價上升幅度下降了5個百分點。……
同比增長率:計算與增長率相關的數據是做資料分析題當中經常遇到的題型,而這類計算有一些常用的速算技巧,掌握這些速算技巧對于迅速解答資料分析題有著非常重要的輔助作用。
增長與同比增長:增長:指量的增加或百分比的增加。同比增長:指和某一相同的時期(比如去年同一時期)進行比較而發生的量的增加或百分比的增加。
增幅與同比增幅:增幅:量和比例的增加幅度,在當前資料分析的考試中,一般等同于增長。同比增幅:量和比例的增加幅度,往往和某一相同的時期(比如去年同一時期)相比較,在當前資料分析的考試中,一般等同于同比增長。
真題一:
全國2007年認定登記和技術合同共計220868項,同比增長7%,總成交金額2226億元,同比增長22.44%;平均每項技術合同成交金額突破百萬元大關,達到100.78萬元。……
136.2007年平均每項技術合同成交金額同比增長率為多少?( )
A. 25.05% B. 35.25% C. 8.15% D. 14.43%
【解析】D 首先,觀察四個選項中的數據差別較大,可以采用估算法。
首先由“2007年認定登記和技術合同共計220868項,同比增長7%”,可知2006年認定登記和技術合同共計≈=200000。又從圖中可知2006年全國技術合同成交金額為18180000萬元,則2006年平均每項技術合同成交金額為18180000÷200000=90.9。又有2007年平均每項技術合同成交金額為100.78萬元,可知同比增長率為(100.78-90.9)÷90.9×100%=9.88÷90.9=0.1+,選D。
真題二:
在1994至2006年間,全國報紙印刷總量持續增長。
以2004年為例,年印刷量在10億對開張以上的企業有30家,其中印刷量增長的企業占90%,而且全部增長5%以上,增長率達兩位數的企業占66.67%。年印刷量在5億至10億對開張之間的企業有26家,其中印刷量增長的有25家,增長率達到兩位數的有19家。
121.2004年印刷量增長率在5%以上的企業有( )家。
A. 19 B. 49 C. 55 D. 無法判斷
【解析】D 題中只是敘述了“年印刷量在10億對開張以上的企業中,印刷量增長的企業和增長率,但是并沒有說全部的企業,因此無法得出2004年印刷量在5%以上的企業個數,選無法判斷。
●資料分析常考規律之二:比重問題
比重問題在資料分析中的表現形式主要有:
***的比重是多少?***的比例是多少?***比重變化幅度最大的是?***比例最高的是?***比例(比重)說法正確的是?等等。
涉及到的知識點:
百分數:表示一個數是另一個數的百分之幾的數,叫百分數。百分數也叫做百分率或百分比。百分數通常不寫成分數的形式,而采用符號“%”(叫做百分號)來表示。如寫為41%、1%。由于百分數的分母都是100,也就是都以1%作單位,便于比較,因此,百分比在工農業生產、科學技術、各種實驗中有著十分廣泛的應用。也是為此,以考查學生能力素質為目的的行政能力測驗之資料分析部分十分清理對百分數的考查,考生要重點掌握。
真題一:
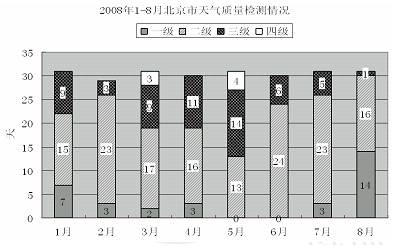
124.第二季度與第一季度相比,空氣達標天數的比重是( )。
A. 上升了3.3% B. 下降了3.3%
C. 上升了12% D. 下降了12%
【解析】D 粗略觀察圖形,第二季度達標天數明顯低于第一季度達標天數,則比重下降。排除A、C。3月份與4月份空氣達標天數不同,則忽略不記,則第一季度空氣達標天數為與第二季度空氣達標天數的差為15+7+23+3-13-24=11天。兩個季度天數都是91天,則第二季度的空氣達標天數與第一季度相比下降幅度為11÷91≈1/9。與選項D最接近。注意,大家應該基礎最基本的1/n(n<20=的小數形式,考場上可以節省很多時間。
真題二:
2006年全國農村外出從業勞動力流向及從業情況統計表(單位:%)
| 全 國 | 東部地區 | 中部地區 | 西部地區 | 東北地區 | |
| 外出從業勞動力從業地區構成 | |||||
| 鄉外縣內 | 19.2 | 29.9 | 13.5 | 15.2 | 26.9 |
| 縣外市內 | 13.8 | 18.4 | 9.9 | 12.4 | 31.5 |
| 市外省內 | 17.7 | 33.1 | 9.0 | 12.8 | 24.2 |
| 省 外 | 49.3 | 18.6 | 67.6 | 59.6 | 17.4 |
| 外出從業勞動力產業構成 | |||||
| 第一產業 | 2.8 | 2.5 | 2.2 | 3.6 | 4.2 |
| 第二產業 | 56.7 | 55.8 | 57.1 | 58.4 | 44.3 |
| 第三產業 | 40.5 | 41.7 | 40.7 | 38.0 | ? |
127.表中“?”處的數值應為( )。
A. 41.6 B. 42.5 C. 51.5 D. 52.4
【解析】C 本題較簡單,三大產業的比重加起來等于1,則第三產業比重為1-(4.2%+44.3%)=51.5%。在考場上,本題只需要粗略估算即可,1-(4.2%+44.3%)中,小數部分為0.5,且百分比要大于50%,直接選C。
第三部分 判斷推理
●判斷推理常考規律之一:疊加與旋轉
圖形推理中疊加與旋轉是常考的兩大規律,疊加分為三類:(1)直接疊加;(2)去同存異;(3)去異存同。旋轉一般是指圖形或圖形中的某些元素在發生有規律的旋轉,旋轉的要點是角度和方向,角度一般為45度、90度、120度、180度你、360度等特殊的容易觀察出來的角度,方向是指在進行逆時針或順時針的旋轉。
真題一:
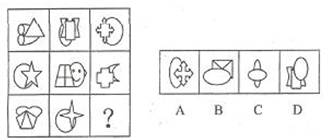
請從所給的四個選項中,選擇最合適的填入問號處,使之呈現一定的規律性:
【解析】 A 此題為疊加與共性規律。 每一行的圖形都是兩個圖形的前后疊加,且都
是直線圖形覆蓋在曲線圖形上,所以選A。
真題二:
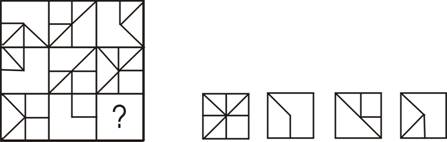
請從所給的四個選項中,選擇最合適的一個填入問號處,使之呈現一定的規律性:
A B C D
【解析】D 圖形疊加中的去同存異。每一行的第一個圖與第二圖疊加后,把相同部分去掉,不同部分留下作為第三個圖。
●判斷推理常考規律之二:圖形共性規律
圖形推理中常考規律有十幾種之多,共性規律出現頻率較高。共性規律是指題干中的圖形具有共同的性質或含有相同的元素。現總結歷年真題中考查共性的題目,給各位考生提供一個思路。
真題一:
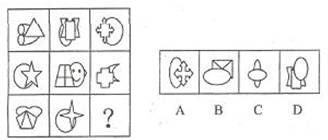
請從所給的四個選項中,選擇最合適的填入問號處,使之呈現一定的規律性:
【解析】 A 題干中的五個圖形的共性是都含有一部分的封閉圖形,但五個圖形都
沒有陰影,排除B項,C、D項都是兩部分的封閉圖形,排除。
真題二:
請從所給的四個選項中,選擇最合適的填入問號處,使之呈現一定的規律性:
【解析】A 每一行的圖形都是兩個圖形的重合,且都是直線圖形覆蓋在曲線圖形
上,所以選A。
【責任編輯:育路編輯 糾錯】