國家公務員網將根據2010年國家公務員考試的最新變化為考生做出有重點的系列指導,第一階段將著重于行測速解技巧的講解,即針對行測各專項重點方法與解題技巧的講解與訓練。為考生講解一個專項,同時提供相關的專項練習,幫助考生快速掌握行測的解題技巧。
國家公務員考試行測每日考點突破系列一——數量關系之數學運算(一)
2010年國家公務員考試已結束,而其中數學運算的復習備考歷來困擾多數考生。國家公務員網專家提醒廣大考生,要徹底走出數學運算低分耗時的困境,在復習和備考、實戰解題時應采用一定的應對策略。總體來說,復習和備考可分為三個階段,一是熟悉題型,二是掌握解題方法和技巧,三是進行一定量的練習,提升解題速度。
實戰解題也要遵循一定的步驟,可用下面的流程圖表示:
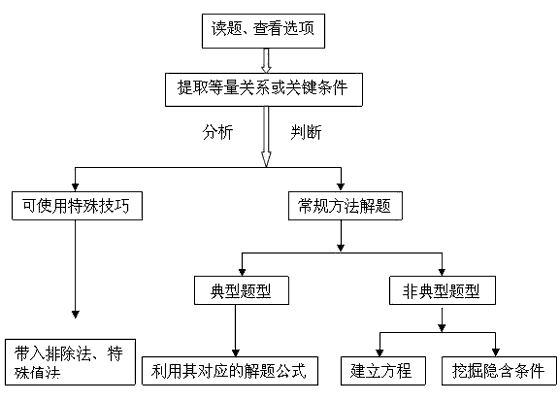
今天我們將就常規方法中的典型題型和非典型題型做出講解。
一、典型題型——公式法
在數學運算中有很多典型題型需要運用數學公式進行計算,如利用等差數列、等比數列的通項及求和公式;平面圖形的周長、面積計算公式;立體圖形的體積、表面積計算公式;平方和、差公式;立方和、差公式等。這些公式一定要牢記于心,不能混淆,避免忙中出錯。
在國家公務員考試中,還有一些廣泛出現的數學運算題型,這些題型的變化相對較少,每一題型都有其核心的解題公式,遇見這類題時,只需理清題意,套用公式即可,如:植樹問題、方陣問題、牛吃草問題……。
下面結合一些典型的試題看看一些公式的使用。
1、基本數學公式的運用
例題1:比較下面三個數的大小:

例題2:甲、乙兩輛汽車在公路上從同一起點朝同一方向同時沿直線前進,在第一秒內,甲車行駛了10米,乙車行駛了2米,此后每一秒內,甲車行駛的距離都比前一秒行駛的距離多20米,乙車行駛的距離都是前一秒行駛距離的2倍,問出發后的第幾秒內的某一時刻,兩車行駛的距離相等?
A.第8秒內
B.第9秒內
C.第10秒內
D.第11秒內

二、具有核心公式的特定題型
例題1:牛吃草問題
在春運高峰時,某客運中心售票大廳站滿等待買票的旅客,為保證售票大廳的旅客安全,大廳入口處旅客排隊以等速度進入大廳按次序等待買票,買好票的旅客及時離開大廳。按照這種安排,如果開10個售票窗口,5小時可使大廳內所有旅客買到票;如果開12個售票窗口,3小時可使大廳內所有旅客買到票,假設每個窗口售票速度相同。由于售票大廳入口處旅客速度增加到原速度的1.5倍,在2小時內使大廳中所有旅客買到票,按這樣的安排至少應開售票窗口數為?
A.15 B.16
C.18 D.19

例題2:方陣問題
某學校全體學生排成方陣練習健身操,已知方陣最外層是104人,問這個學校共有多少人?
A.729 B.784
C.676 D.841
解題分析:這是典型的方陣問題,是各類公務員考試的常考題型。解題時需要抓住方陣問題的核心解題公式:
方陣最外層總人數=方陣最外層每邊人數×4-4
方陣總人數=最外層每邊人數的平方
直接套用公式可得該方陣最外層每邊人數=(104+4)÷4=27,方陣總人數=272=729。
此題答案為A。
例題3:多次相遇問題
甲、乙兩人同時從A、B兩地出發,相向而行,甲到達B地后,立即往回走,回到A地后,又立即向B地走去;乙到達A地后,立即往回走,回到B地后,又立即向A地走去。二人如此往復,已知整個過程中,二人行走速度不變,兩人第二次迎面相遇地點距離A地500米,第四次迎面相遇地點距離B地600米,問A、B兩地相距多少米?
A.1 200 B.980
C.900 D.1 060

二、非典型題型——方程法
方程法,即設未知數列方程解應用題,是解決數學運算題的普遍方法。方程法的解題步驟如下:
第一步,分析題中等量關系;
第二步,合理設未知數,將未知量用未知數準確表示;
第三步,根據等量關系組建方程(組),解方程得到所求量。
在公務員考試中,所列方程通常都是一元一次方程或二元一次方程,有時可能是方程(組),需要培養快速解方程的能力。
例題1:某地水費,不超過10度時,每度0.45元,超過10度時,超過的部分每度0.80元,張家比李家多交水費3.30元,如果兩家的用水量都是整數度,問張家、李家共用電多少度?
A.21 B.23
C.25 D.27
解題分析:此題要求出張家、李家共用電多少度,因此必須求出張家、李家各用電多少度。因為張家比李家多交水費3.30元(330分),而330不是45的整數倍,也不是80的整數倍,因此可知一定是張家用水量超過10度,李家則不到10度。題中的等量關系較為簡單,即張家所交水費-李家水費=3.3元,可通過列方程求解。
設未知數也無需選擇,直接設張家用水x度,李家用水y度,則x>10,y<10,根據題意有45×10+80×(x-10)-45y=330,化簡得16x=9y+136。
這是一個不定方程,但由于未知數都是有特定范圍的整數,因此可以運用整除特性來確定x、y的具體值。
分析16x=9y+136這個式子,等式左邊能整除16,因此等式右邊也要求能整除16,136除以16的余數是8,因此9y除以16的余數應是16-8=8,由于y<10,簡單取值檢驗知,當且僅當y=8時符合題意,此時代入可求得x=13,張家、李家共用電8+13=21度。
此題答案為A。
例題2:某項工程,甲、乙兩人合作5天后,乙、丙兩人再一起合作2天,工程還剩下1/180;若乙先工作6天,甲、丙兩人合作4天后,工程還剩下2/45;若按甲、乙、丙的順序輪流工作,14天后工程還剩下1/36;問若乙先完成工程的1/36,甲、丙合作還需要多少天可完成余下工程?
A.7.5 B.7
C.6 D.6.5
解題分析:這是一個典型的工程問題,是公務員考試的常見題型。工程問題中的等量關系是:工作效率×工作時間=工作量、各部分的工作量之和等于總工作量。此題給出了三種不同的合作方式,可通過設未知數列方程組,求得三人的工作效率,然后在通過計算得出所求。第三種合作方式實際就是甲和乙工作了5天,丙工作了4天。
具體解題過程如下:
設甲、乙、丙三人的工作效率依次是x、y、z,依題意有:
5(x+y)+2(y+z)=1-1/180
6y+4(x+z)=1-2/45
5x+5y+4z=1-1/36
解方程組通常采用消元法,考慮到題目最后所求,需要知道甲、丙的工作效率,因此此處消去未知數y,得到x、z的值。
解得x=1/12、z=1/18,(y=1/15)
甲、丙合作一天完成5/36,所求即為(1-1/36)÷(5/36)=7天。
此題答案為B。