2007年中考復習：平面幾何添加輔助線的技巧

　　近兩年，中考數學試卷中降低了對平面幾何的要求，但就此認為對于學生的思維訓練可以放松，那就錯了。數學始終應包含其特有的知識、思想與方法、活動應用、知識審美等四個層面，而培養一名學生嚴密的邏輯思維能力和推理論證能力更是一刻不離地貫穿其中的。

　　不少初中生感到平面幾何比較難學，特別是遇到需要添加輔助線的習題，有時會感到無從下手。在此，我們對初中幾何中添加輔助線的思路從以下幾個方面進行了總結，希望能幫助參加中考的學生有效復習備考。

　　揭示圖形中隱含的性質(擴大原題的“已知”)

　　當題目的題設和結論之間的邏輯關系不太明朗、甚至“彼此孤立”時，可以通過添加適當的輔助線，把題設條件中隱含的有關性質充分顯現出來，擴大了已知條件，從而有利于迅速找到題目的最近切入口，進而推導出題目的結論。

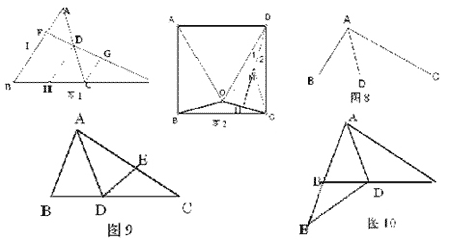
　　【例題1】如圖1，D是⊿ABC的邊AC的中點，延長BC到點E，使CE=BC，ED的延長線交AB于點F，求ED∶EF

　　分析：思路一：過C作AB的平行線交DE于G，由D是AC的中點可得FD=DG，由CE=BC可得FG=GE，從而得ED∶EF=3∶4

　　思路二：過D作BE的平行線交AB于I，類似法一得ID∶BC=1∶2，ID∶BE=1∶4，從而得ED∶EF=3∶4

　　思路三：過D作AB的平行線交BE于H，易得BH=HC=1/4BE，得ED∶EF=3∶4

　　說明：本題三種思路所添加的三條平行線，均是為了充分利用“D是⊿ABC的邊AC的中點”這一條件，使本來感覺比較薄弱的一個條件，在平行線的作用下變得內涵豐富，既有另外一邊的中點出現，又可以利用三角形的中位線定理，這樣使用起來就更加得心應手。

　　構造圖形，補題設(已知)的不足有時必須添加一些圖形，使題設條件能充分顯示出來，從而為定理的應用創造條件，或者使不能直接證得的結論轉化為與它等價的另一個結論，便于思考與證明。

　　【例題2】已知：O是正方形ABCD內一點，∠OBC=∠OCB=15°求證：⊿AOB是等邊三角形

　　分析：(如圖2)構建三角形OMC。使DH⊥OC于H，則∠2=15°作∠DCM=15°則⊿DMC≌⊿BOC且∠MCO=60°DM=MC=OC=OM

　　∴∠DMO=360°-60°-150°=150°

　　∴∠1=∠MOD=15°

　　從而有∠DOC=∠DCO=75°，DO=DC=AD=AB=AO

　　說明：本題就是利用輔助線構造出一個和要證明的結論類似的等邊三角形，然后借助構造出的圖形解答題目。

　　把分散的幾何元素聚集起來

　　有些幾何題，條件與結論比較分散。通過添加適當的輔助線，將圖形中分散、“遠離”了的元素聚集到有關的圖形上，使他們相對集中、便于比較、建立關系，從而找出問題的解決途徑。

　　【例題3】如圖8,△ABC中，∠B=2∠C，且∠A的平分線為AD，問AB與BD的和等于AC嗎?

　　思路一：如圖9，在長線段AC上截取AE=AB，由△ABD≌△AED推出BD=DE，從而只需證EC=DE.

　　思路二：如圖10，延長短線段AB至點E,使AE=AC，因而只需證BE=BD,由△AED≌△ACD及∠B=2∠C，可證∠E=∠BDE，從而有BE=BD.

　　思路三：如圖10，延長AB至E，使BE=BD，連接ED，由∠ABD=2∠C，∠ABD=2∠E，可證△AED≌△ACD，可得AE=AC,即AC=AB+BD.

　　說明：這道例題就是利用輔助線，把本來不在一條直線的線段AB與BD聚集到一條直線上來，這樣就可以輕松得到AB+BD或者AC——AB,然后題目就迎刃而解了。

　　平面幾何中添加輔助線的方法是靈活多變的，這就要求我們熟練掌握數學中的基本概念和基本定理，在實踐探索中經常進行歸類總結，仔細分析題目給我們的條件，找到隱含的及一些有規律的信息。