公考行測:數(shù)量關(guān)系之“全錯(cuò)位排列”真題剖析
來源:發(fā)布時(shí)間:2011-06-15 [an error occurred while processing this directive]
作為排列組合試題的一種特殊類型,全錯(cuò)位排列在公考中也偶有出現(xiàn)。因?yàn)檩^之其他題型來說,全錯(cuò)位排列的原理需要結(jié)合舉例子遞推出來,故考生朋友們理解起來有一定的困難。在此京佳崔熙琳老師將考試中出現(xiàn)過的該類題型進(jìn)行匯總,希望給各位考生提供一些幫助。
公考行測:數(shù)量關(guān)系之“全錯(cuò)位排列”經(jīng)典真題剖析
一、全錯(cuò)位排列遞推公式的推導(dǎo)
把編號從1到n的n個(gè)小球放到編號為從1到n的n個(gè)盒子里,假定每個(gè)盒子中的小球編號與盒子的編號不得一樣(即:1號球不在1號盒,2號球不在2號盒,依次類推),請問共有幾種放法?
用列舉法進(jìn)行公式的推導(dǎo):
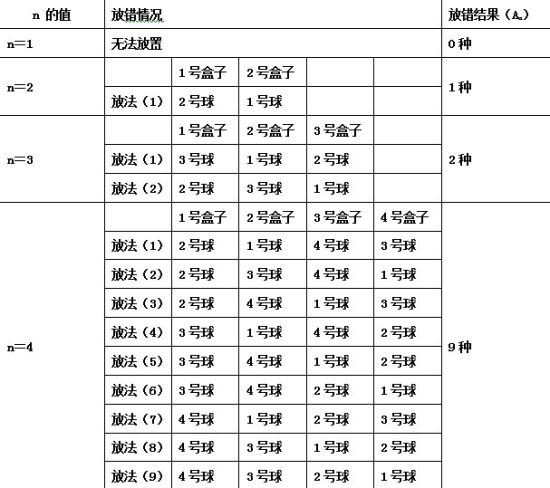
通過圖1可以發(fā)現(xiàn),An與n存在如下的遞推關(guān)系:
An=(An-2+A n-1)×(n-1)(其中,n≥3,且A 1=0,A 2=1)
此遞推公式可以產(chǎn)生一個(gè)全錯(cuò)位排列的結(jié)果數(shù)列:
A1=0;
A2=1;
A3=(A1+A2)×(3-1)=2;
A4=(A2+A3)×(4-1)=9;
A5=(A3+A4)×(5-1)=44;
A6=(A4+A5)×(6-1)=265…………
考生在遇到全錯(cuò)位排列試題時(shí)候只需要按照上述遞推公式進(jìn)行簡單推導(dǎo)即可求出結(jié)果。
二、真題解析
例1:(2011年浙江省考真題55題)
四位廚師聚餐時(shí)各做了一道拿手菜。現(xiàn)在要求每個(gè)人去品嘗一道菜,但不能嘗自己做的那道菜。問共有幾種不同的嘗法?
A.6種 B.9種 C.12種 D.15種
「答案與解析」B.此題為全錯(cuò)位排列試題。根據(jù)全錯(cuò)位排列公式“An=(An-2+A n-1)×(n-1)(其中,n≥3,且A 1=0,A 2=1)”,可知,當(dāng)n=4時(shí),共有9種嘗法。
例2:(2010年某省考試真題)
五個(gè)瓶子都貼了標(biāo)簽,其中恰好貼錯(cuò)了三個(gè),則錯(cuò)的可能情況共有多少種?
A.5 B. 10 C. 15 D. 20
「答案與解析」D.做此類題目時(shí)通常分為兩步:第一步,從五個(gè)瓶子中選出三個(gè),共有C(3,5)=10種選法;第二步,將三個(gè)瓶子全部貼錯(cuò),根據(jù)上表有2種貼法。則恰好貼錯(cuò)三個(gè)瓶子的情況有10×2=20種。
【責(zé)任編輯:育路編輯 糾錯(cuò)】


