考研數學：洛必達法則求抽象函數極限易犯錯誤

 　　考研數學：洛必達法則求抽象函數極限易犯錯誤

　　函數極限的計算是考研數學中的一個高頻考點，每年都會出題。計算函數極限的方法很多，如：利用極限的基本性質、兩個重要極限、等價無窮小代換、洛必達法則、泰勒公式、恒等變形等，其中洛必達法則是重要的方法之一，經常用于函數極限的計算之中，但有些同學在運用洛必達法則時容易出現(xiàn)錯誤，沒有正確掌握其使用方法，下面文都教育考研數學的蔡老師對使用洛必達法則求抽象函數的極限時容易犯的錯誤做些分析，供考研的同學復習參考。

　　一、使用洛必達法則求抽象函數的極限時容易犯的錯誤

　　對于抽象函數的極限，運用洛必達法則計算時容易出現(xiàn)下面這樣的錯誤：

1、題目條件只是告訴了函數

連續(xù)，并未說明可導，因此，在求極限過程中運用洛必達法則對函數進行求導是錯誤的; 2、題目雖然告訴了函數

可導，但不知導數是否連續(xù)，因此，把導函數當成連續(xù)的函數來求極限是錯誤的。

　　下面通過一些具體例題來說明這些錯誤是如何發(fā)生的，以及應該怎么避免。

　　二、典型題型分析

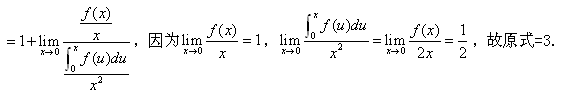
　　上面的分析和具體例題提醒我們，雖然洛必達法則是一個很有用的、重要的求函數極限的工具，但在運用洛必達法則求函數極限時，一定要仔細審視函數是否滿足洛必達法則的使用條件，不要理所當然地認為或默認所有函數都符合其運用條件，尤其是求抽象函數的極限時要特別小心，不要出現(xiàn)不該犯的錯誤，從而導致在考試中丟分。

　　關鍵詞：考研數學 洛必達法則 函數極限