破解考研數學重災區：中值定理證明思路小結

 　　破解考研數學重災區：中值定理證明思路小結

　　還有不到40天就到了2016考研初試的時間了，為了讓學生能夠更好地應對考研，本文將討論一下中值定理這塊的相應證明題的一般解題思路。

　　中值定理這塊一直都是很多考生的"災難區"，一直沒有弄清楚看到一個題目到底怎么思考處理，因此也是考研得分比較低的一塊內容，如果考生能把中值定理的證明題拿下，那么我們就會比其他沒做上的同學要高一個臺階，也可以說這是一套"拉仇恨"的題目。下面跨考教育數學教研室佟老師就和大家來一起分析一下這塊內容。

　　一、具體考點分析

　　首先我們必須弄清楚這塊證明需要的理論基礎是什么，相當于我們的工具，那需要哪些工具呢?

　　第一：閉區間連續函數的性質。

　　比較值定理：閉區間連續函數的必有比較大值和比較小值。

　　推論：有界性(閉區間連續函數必有界)。

　　介值定理：閉區間連續函數在比較大值和比較小值之間中任意一個數，都可以在區間上找到一點，使得這一點的函數值與之相對應。

　　零點定理：閉區間連續函數，區間端點函數值符號相異，則區間內必有一點函數值為零。

　　第二：微分中值定理(一個引理，三個定理)

　　費馬引理：函數f(x)在點ξ的某鄰域U(ξ)內有定義，并且在ξ處可導，如果對于任意的x∈U(ξ)，都有f(x)≤f(ξ) (或f(x)≥f(ξ) )，那么f'(ξ)=0。

　　羅爾定理：如果函數f(x)滿足：

　　(1)在閉區間[a,b]上連續;

　　(2)在開區間(a,b)內可導;

　　在區間端點處的函數值相等，即f(a)=f(b

　　那么在(a,b)內至少有一點ξ(a<ξ，使得 f?(ξ)="0.

　　幾何上，羅爾定理的條件表示，曲線弧 (方程為 )是一條連續的曲線弧 ，除端點外處處有不垂直于x軸的切線，且兩端點的縱坐標相等。而定理結論表明：

　　弧上至少有一點 ，曲線在該點切線是水平的。

　　拉格朗日中值定理：如果函數f(x)滿足：

　　(1)在閉區間[a,b]上連續;

　　(2)在開區間(a,b)內可導;

　　在區間端點處的函數值相等，即f(a)=f(b)，

　　那么在(a,b)內至少有一點ξ(a<ξ

　　加強版：如果函數 f(x) 在積分區間[a, b]上連續，則在 (a, b)上至少存在一個點 ξ，使下式成立

　　第四：變限積分求導定理： 如果函數f(x)在區間[a，b]上連續，則積分變上限函數在[a,b]上具有導數，并且導數為：

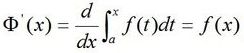
　　第五：牛頓--萊布尼茨公式：如果函數f(x) 在區間[a,b] 上連續，并且存在原函數F(x) ，則

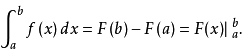
　　以上定理要求理解并掌握定理內容和相應證明過程。

　　二、注意事項

　　針對上文中具體的考點，佟老師再給出幾點注意事項，這幾個注意事項也是在證明題中的"小信號"，希望大家理解清楚并掌握：

　　1. 所有定理中只有介值定理和積分中值定理中的ξ所屬區間是閉區間。

　　2. 拉格朗日中值定理是函數f(x)與導函數f'(x)之間的橋梁。

　　3. 積分中值定理是定積分與函數之間的橋梁。

　　4. 羅爾定理和拉格朗日中值定理處理的對象是一個函數，而柯西中值定理處理的對象是兩個函數，如果結論中有兩個函數，形式與柯西中值定理的形式類似，這時就要想到我們的柯西中值定理。

　　5. 積分中值定理的加強版若在定理證明中應用，必須先證明。

　　其次對于中值定理證明一般分為兩大類題型：第一應用羅爾定理證明，也可又分為兩小類：證明結論簡單型和復雜型，簡單型一般有證明f'(ξ)=0，f'(ξ)=k (k為任意常數)，f'(ξ1)=g'(ξ2)，f''(ξ)=0，f''(ξ)=g''(ξ)，

　　像這樣的結論一般只需要找羅爾定理的條件就可以了，一般羅爾定理的前兩個條件題目均告知，只是要需找兩個不同點的函數值相等，需找此條件一般會運用閉區間連續函數的性質、積分中值定理、拉格朗日中值定理、極限的性質、導數的定義等知識點。復雜型就是結論比較復雜，需要建立輔助函數，再使輔助函數滿足羅爾定理的條件。輔助函數的建立一般借助于解微分方程的思想。第二就是存在兩個點使之滿足某表達式。這樣的題目一般利用拉格朗日中值定理和柯西中值定理，處理思想把結論中相同字母放到等是一側首先處理。

　　比較后希望同學們仔細研究這塊內容的歷年真題，通過研究真正的把處理方法轉化為自己的，跨考教育祝大家考研成功!